The Maxwell-Boltzmann Distribution

 

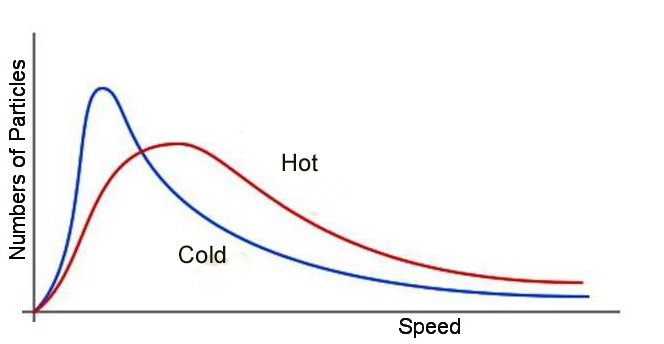
The Maxwell-Boltzmann: This graph depicts the relative number of particles in a system as a function of their speed. In an ideal gas, the average speed arises with temperatures. The number of particles with the highest speeds is small, due to exponential decay.

According to the second law of thermodynamics, the function of the energy distribution in equilibrium will result in a maximum value for entropy, that is, both the number of microstates, W, and the entropy as defined by Clausius will be at a maximum. From the derivation of this distribution (see Appendix A-4), a bell-like speed distribution, called the Maxwell-Boltzmann curve, is obtained (see Fig). In statistics, a bell curve is often referred to as a “normal distribution.” (It is worth noting that the normal distribution, without the long tail to the right, is an approximation of the Maxwell-Boltzmann distribution that is shown in the figure, and is the most common distribution in nature.) In the normal distribution, the probability that an atom will have a given energy decreases exponentially as the energy rises.

The bell-like Maxwell-Boltzmann distribution is derived from the exponential decay of the number of particles with a given energy. That is, the relative number of particles carrying a particular energy decreases exponentially as the energy rises according to exp(-E/kT)  (k is the Boltzmann constant, E is the energy and T is the temperature). It follows that most of the particles possess low energy. Multiplication of the increased energy  by the exponentially decreasing number of particles yields an energy distribution which is a rising function at low energies and a falling function at high energies. The result is a bell-like distribution.

The exponential decay is drastic: the number of deviations from the average decreases rapidly: most of the particles in the distribution have energy close to the average. Many phenomena in nature give the average the highest probability; however, there are also some distributions in nature which give substantial probability to the extremes. These distributions, the “long tail distributions,” will be discussed in detail further on.

Maxwell-Boltzmann distribution is the origin of the “wisdom of the crowd” as the opinion of the majority is considered as the right answer. This distribution is found in IQ tests, human heights etc. pp 75-86.