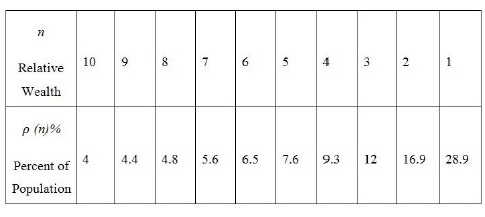
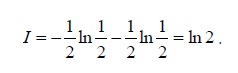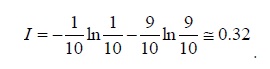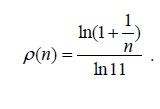The Carnot
The Clausius
The Boltzmann
The Gibbs
Misconceptions related to Entropy

Heat
heat is energy stored in a body
NOT TRUE
The energy that is stored in a body is called internal energy. Heat is the energy removed from a body or added to it. Heat is similar to work. There is no work inside a body: work can be applied on a body or can be applied by a body.
Why this error is significant to the understanding of entropy? Entropy is defined as heat divided by temperature. Since temperature is a property of a body, therefore entropy is of the same nature as heat and work.
This is very significant as we will see later.

Disorder
Entropy is a measure of disorder
NOT TRUE
Entropy is the logarithm of the number of the microstates of a thermally isolated system.
The number of the microstates is the number of possible distinguishable ways in which a statistical system can be found.
Therefore, entropy is a measure of complexity and uncertainty of a system and NOT disorder.

Entropy
Entropy production in an irreversible process is higher than in that of a similar process done in reversible way
NOT TRUE
This mistake comes from our intuition that the entropy is generated in an irreversible operation (which is true). Nevertheless, entropy is defined in equilibrium where Q/T has a maximal value. Namely,
S≡ (Q/T)reversible
and the second law states that:
S ≥ (Q/T)
Which means that heat divided by temperature is biggest in reversible operation and not
(Q/T)irreversible > (Q/T)reversible !

The Second Law
The second law increases disorder
NOT TRUE
This error comes from our intuition that it is much easier to break things than to fix them. If we put a cube of sugar in a glass of tea, the sugar will dissolve. It requires much work to obtain back sugar cube from a glass of sweeten tea. However, there are opposite examples, i.e. emulsion of oil and water will spontaneously be separated into two nice layers of oil and water.
Many believe that disorder increases spontaneously because it is a common belief. However if we look around us we see that “order” increases all the time. Lord Kelvin, a famous 19th century scientist, claimed that objects heavier than air (namely objects that their specific density is higher than that of air) cannot fly. He made this colossal mistake not because he did not know about Bernoulli law (that is forgivable…) but because he did not look at the birds in the sky! Like most people he saw birds flying but he never related their flight to physics.
Order is generated all around us, and spontaneous generation of order should be explained by physics.

Shannon entropy
Shannon entropy has nothing to do with physical entropy
NOT TRUE
Everything in our world is energy. Therefore, when a file is transferred from a transmitter to a receiver, it is bound by the laws of thermodynamics.
If we use pulses for the energetic bits for the file transmission (EM pulse is a classic oscillator), the transferred energy from the hot transmitter to the cold receiver is a thermodynamic process in which Shannon entropy is the amount of the increase of Gibbs entropy of the process.

Negative Entropy
Shannon information is negative entropy
NOT TRUE
Shannon information IS entropy. The reason for this common error is the confusion between information a-la Shannon that is defined as the logarithm of the number of the possible different transmitted files and our intuition that information is ONE specific file. In our book a specific transmitted file (which is a microstate) is called content. Therefore Shannon information is the logarithm of the number of all possible contents.